Bilateral Multi-Perspective Matching for Natural Language Sentences

ZhiguoWang,Wael Hamza, Radu Florian IBM T.J.Watson Research Center arXiv 2017

Points

• Natural language sentence matching is a fundamental technology for a variety of tasks.
• Given two sentences P and Q, our model first encodes them with a BiLSTM encoder.
• We match the two encoded sentences in two directions P→Q and P←Q. In each matching direction, each time step of one sentence is matched against all time-steps of the other sentence from multiple perspectives. Then, another BiLSTM layer is utilized to aggregate the matching results into a fix-length matching vector.
• Based on the matching vector, the decision is made through a fully connected layer.
• We evaluate our model on three tasks: paraphrase identification, natural language inference and answer sentence selection(achieves the state-of-the-art performance on all tasks).

Models

• Overview
  

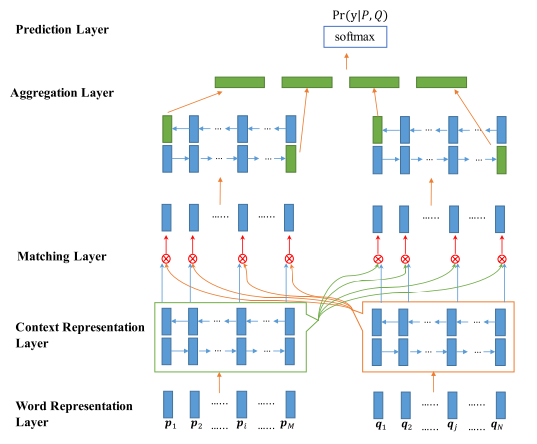
$\otimes$ is multi-perspective matching operation. $m=f_m(v_1,v_2;W)$, where $v_1$ and $v_2$ are two $d$ dimensional vectors, $W\in R^{l\times d}$ is a trainable parameter, $l$ is the number of perspectives, and the returned $m$ is a $l$ dimensional vector. $m_k=cosine(W_k\circ v_1, W_k\circ v_2)$

• Full Matching
  

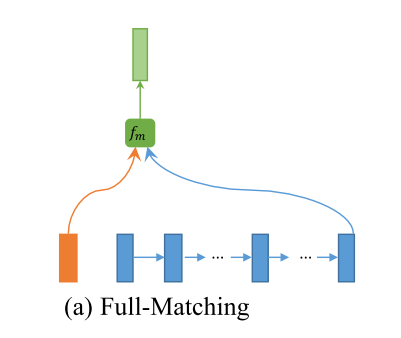
In this strategy, each forward (or backward) contextual embedding $h_i^p$ is compared with the last time step of the forward (or backward)representation of the other sentence $h_N^q$. $m_i^{full}=f_m(h_i^p, h_N^q; W)$

• Maxpooling Matching
  

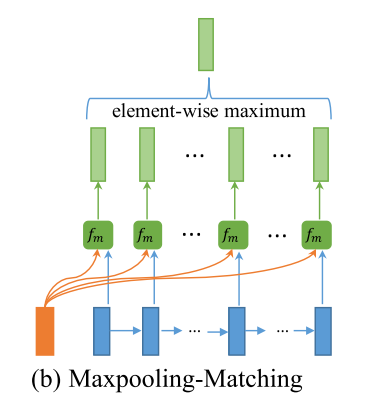
In this strategy, each forward (or backward) contextual embedding $h_i^p$ is compared with every forward contextual embeddings of the other sentence $h_j^q$ for $j \in (1…N)$, and only the maximum value of each dimension is retained. $mi^{max}=max{j\in (1\cdots N)} f_m(h_i^p, h_j^q; W)$

• Attentive Matching
  

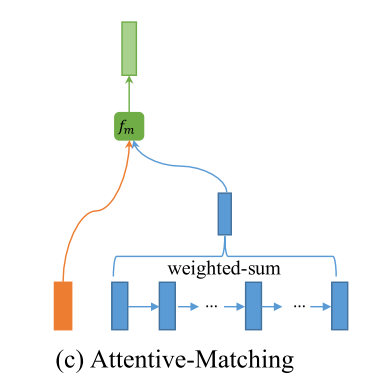
First calculate the cosine similarities between each forward contextual embedding $h_i^p$ and every forward contextual embeddings of the other sentence $hj^q$: $\alpha{i,j}=consine(h_i^p, h_j^q), j=1, \cdots, N$

Then, take $\alpha_{i,j}$ as the weight of $h_j^q$ and calculate an attentive vector for the entire sentence Q by weighted summing all the contextual embeddings of Q: $hi^{mean}=\frac{\sum{j=1}^{N}\alpha_{i,j}\dot hj^q}{\sum{j=1}^N\alpha_{i,j}}$

Finally, we match each forward contextual embedding of $h_i^p$ with its corresponding attentive vector: $m_i^{att}=f_m(h_i^p, h_i^{mean}; W)$

• Max Attentive Matching
  

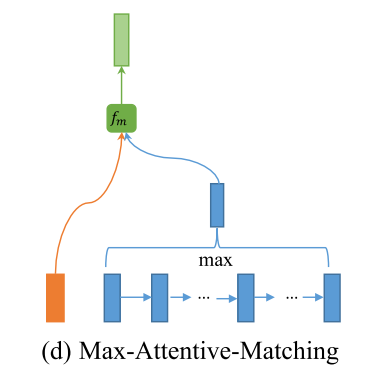
Instead of taking the weighed sum of all the contextual embeddings as the attentive vector, they pick \alert{the contextual embedding with the highest cosine similarity} as the attentive vector. Then, we match each contextual embedding of the sentence P with its new attentive vector.

Experiments on Paraphrase Identification