A Survey of Attention

Some papers about Attention in NLSM

Introduction

What and Why

Reference: http://www.wildml.com/2016/01/attention-and-memory-in-deep-learning-and-nlp/

• What is Attention Mechanisms

  Attention Mechanisms in Neural Networks are (very) loosely based on the visual attention mechanism found in humans. There exist different models come down to being able to focus on a certain region of an image with “high resolution” while perceiving the surrounding image in “low resolution”, and then adjusting the focal point over time.

• Why we need Attention Mechanisms

  It seems somewhat unreasonable to assume that RNN can encode all information about a potentially very long sentence into a single vector.

• How does Attention Mechanisms work

  With an attention mechanism we no longer try encode the full source sentence into a fixed-length vector. Rather, we allow the decoder to “attend” to different parts of the source sentence at each step of the output generation.

show

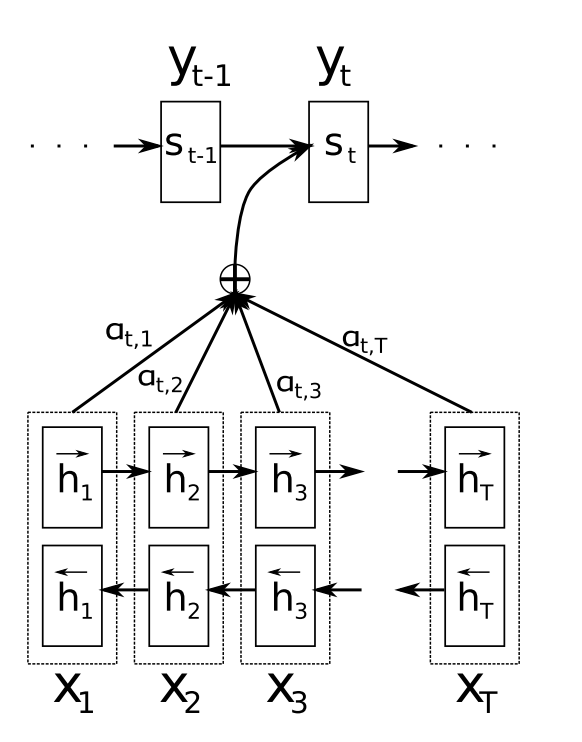
The important part is that each decoder output word $yt$ now depends on a weighted combination(sum to 1) of all the input states, not just the last state. The $a$’s are weights that define in how much of each input state should be considered for each output. So, if $a{3,2}$ is a large number, this would mean that the decoder pays a lot of attention to the second state in the source sentence while producing the third word of the target sentence.

Papers

Bilateral Multi-Perspective Matching for Natural Language Sentences

ZhiguoWang,Wael Hamza, Radu Florian IBM T.J.Watson Research Center arXiv 2017

Points

• Natural language sentence matching is a fundamental technology for a variety of tasks.
• Given two sentences P and Q, our model first encodes them with a BiLSTM encoder.
• We match the two encoded sentences in two directions P→Q and P←Q. In each matching direction, each time step of one sentence is matched against all time-steps of the other sentence from multiple perspectives. Then, another BiLSTM layer is utilized to aggregate the matching results into a fix-length matching vector.
• Based on the matching vector, the decision is made through a fully connected layer.
• We evaluate our model on three tasks: paraphrase identification, natural language inference and answer sentence selection(achieves the state-of-the-art performance on all tasks).

Models

• Overview
  

$\otimes$ is multi-perspective matching operation. $m=f_m(v_1,v_2;W)$, where $v_1$ and $v_2$ are two $d$ dimensional vectors, $W\in R^{l\times d}$ is a trainable parameter, $l$ is the number of perspectives, and the returned $m$ is a $l$ dimensional vector. $m_k=cosine(W_k\circ v_1, W_k\circ v_2)$

• Full Matching
  

In this strategy, each forward (or backward) contextual embedding $h_i^p$ is compared with the last time step of the forward (or backward)representation of the other sentence $h_N^q$. $m_i^{full}=f_m(h_i^p, h_N^q; W)$

• Maxpooling Matching
  

In this strategy, each forward (or backward) contextual embedding $h_i^p$ is compared with every forward contextual embeddings of the other sentence $h_j^q$ for $j \in (1…N)$, and only the maximum value of each dimension is retained. $mi^{max}=max{j\in (1\cdots N)} f_m(h_i^p, h_j^q; W)$

• Attentive Matching
  

First calculate the cosine similarities between each forward contextual embedding $h_i^p$ and every forward contextual embeddings of the other sentence $hj^q$: $\alpha{i,j}=consine(h_i^p, h_j^q), j=1, \cdots, N$

Then, take $\alpha_{i,j}$ as the weight of $h_j^q$ and calculate an attentive vector for the entire sentence Q by weighted summing all the contextual embeddings of Q: $hi^{mean}=\frac{\sum{j=1}^{N}\alpha_{i,j}\dot hj^q}{\sum{j=1}^N\alpha_{i,j}}$

Finally, we match each forward contextual embedding of $h_i^p$ with its corresponding attentive vector: $m_i^{att}=f_m(h_i^p, h_i^{mean}; W)$

• Max Attentive Matching
  

Instead of taking the weighed sum of all the contextual embeddings as the attentive vector, they pick \alert{the contextual embedding with the highest cosine similarity} as the attentive vector. Then, we match each contextual embedding of the sentence P with its new attentive vector.

Experiments on Paraphrase Identification

Inner Attention based Recurrent Neural Networks for Answer Selection

BingningWang, Kang Liu, Jun Zhao Institute of Automation Chinese Academy of Sciences ACL 2016

Points

• Attention based recurrent neural networks in representing natural language sentences.
• Analyze the deficiency of traditional attention based RNN models quantitatively and qualitatively.
• Present three new RNN models that add attention information before RNN hidden representation.
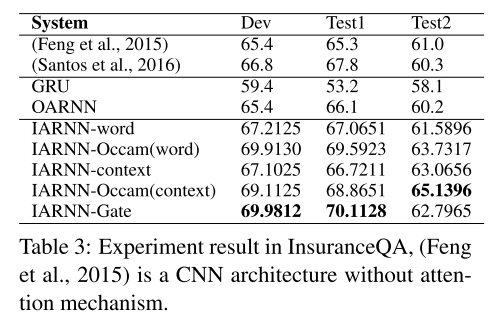
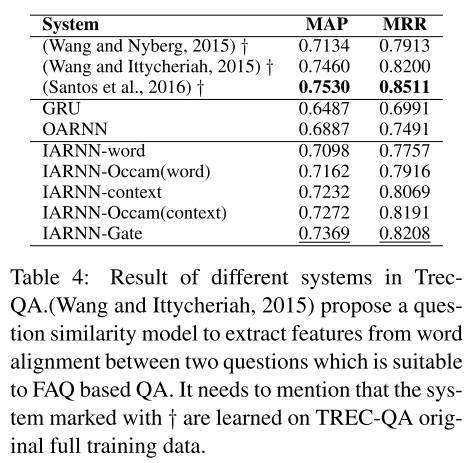
• Experimental results show advantage in repre- senting sentence and achieves new state-of-art results in answer selection task.

Traditional Attention based RNN Models

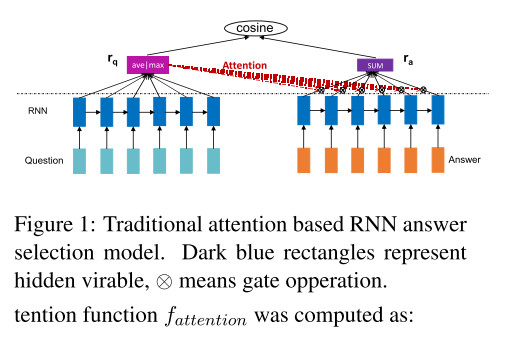
$H_a=[h_a(1),h_a(2),\cdots, h_a(m)]$

$m(t)=tanh(W_{hm}ha(t)+W{qm}r_q)$

$f_{attention}(r_q, ha(t))=exp(w{ms}^Tm(t))$

$st\propto f{attention}(r_q, h_a(t))$

$\tilde{h}_a(t)=h_a(t)s_t$

$ra=\sum{t=1}^m\tilde{h}_a(t)$

answer sentence representation $r_a$ may be represented in a question-guided way: when its hidden state $h_a(t)$ is irrelevant to the question (determined by attention weight $s_t$), it will take less part in the final representation; but when this hidden state is relavent to the question, it will contribute more in representing $r_a$.

IARNN WORD

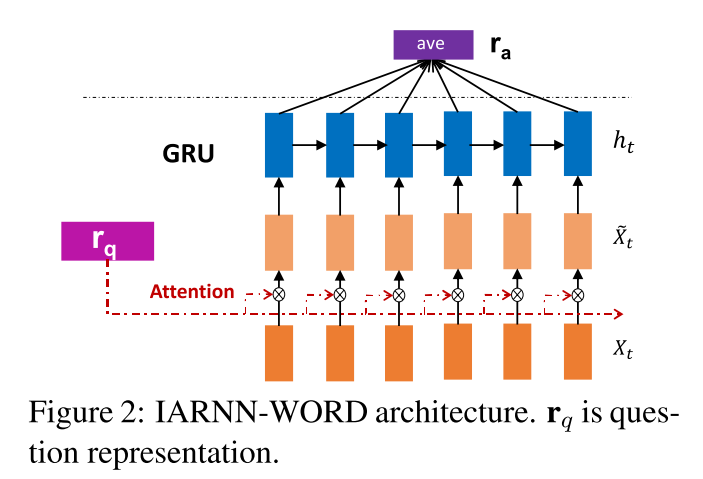
$\alpha_t=\sigma(rq^TM{qi}x_t)$

$\tilde{x}_t=\alpha_t*x_t$

$M_{qi}$ is an attention matrix to transform a question representaion into the word embedding space. Then we use the dot value to determine the question attention strength, $\theta$ is sigmoid function to normalize the weight $\alpha_t$ between 0 and 1.

IARNN CONTEXT

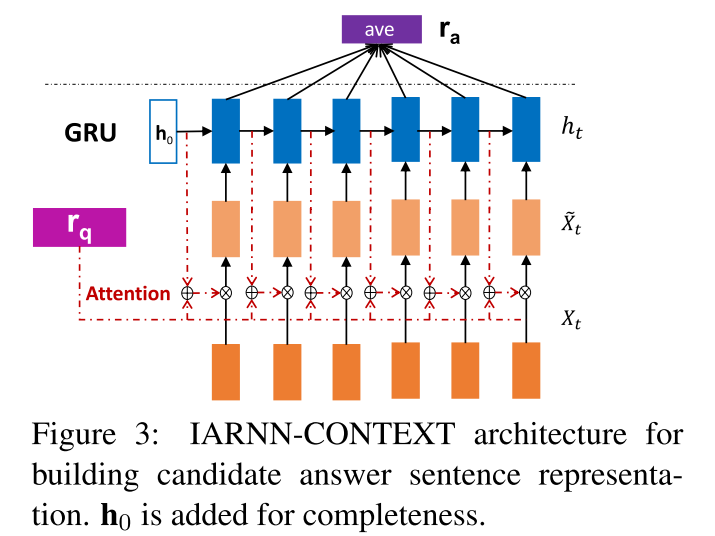
$wC(t)=M{hc}h{t-1}+M{qc}r_q$

$\alpha_C^t=\sigma(w_C^T(t)x_t)$

$\tilde{x}_t=\alpha_C^t\ast x_t$

Use $h{t−1}$ as context, $M{hc}$ and $M_{qc}$ are attention weight matrices, $w_C(t)$ is the attention representation which consists of both question and word context information.

IARNN GATE

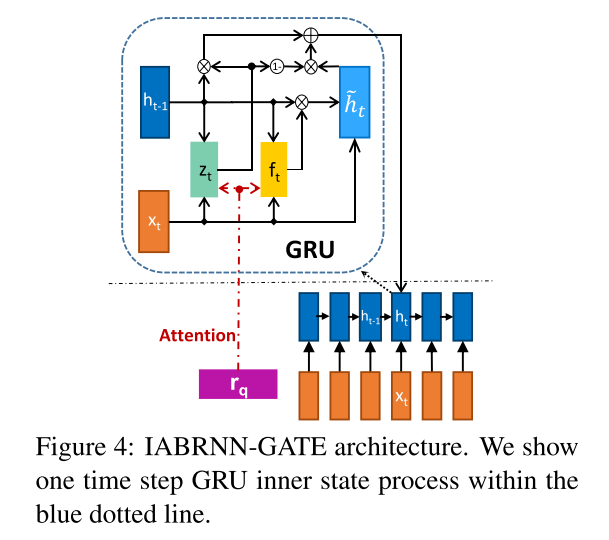
$zt=\sigma(W{xz}xt+W{hz}h{h-t}+M{qz}r_q)$

$ft=\sigma(W{xf}xt+W{hf}h{t-1}+M{qf}r_q)$

$\tilde{h}t=tanh(W{xh}xt+W{hh}(ft\odot h{t-1}))$

$h_t=(1-zt)\odot h{t-1}+z_t\odot \tilde{h}_t$

$M{qz}$ and $M{hz}$ are attention weight matrices. In thisway, the update and forget units in GRU can focus on not only long and short term memory but also the attention information from the question.

IARNN OCCAM

I don’t know what is it.

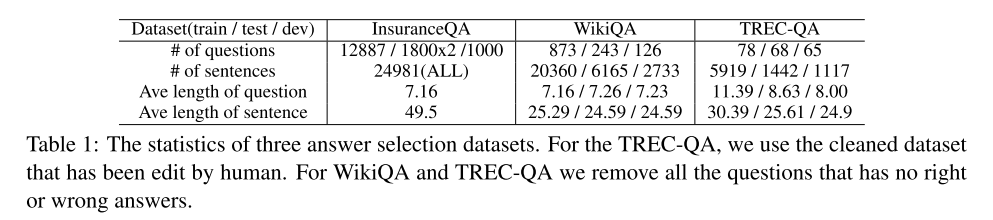
Experiments

To be continued…